Advances in biostatistics and computing have led to the creation of novel types of machine learning algorithms for clinical outcome prediction models. Three clinically and statistically robust models include artificial neural networks, fuzzy logic and bayesian analysis. These techniques complement classical approaches of regression analysis and decision tree analysis. This editorial explains the novel outcome prediction system using Bayesian neural networks with fuzzy logic. This novel approach can be practically applied to both clinical and non-clinical settings.
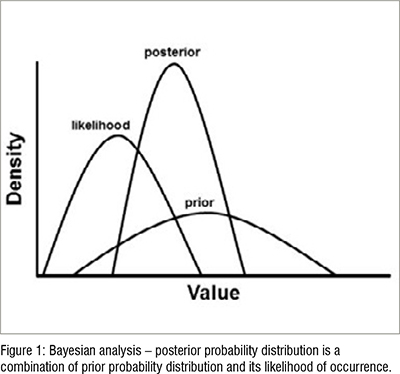
Bayesian analysis enables incorporation of new data with existing knowledge. Based on this knowledge, the researcher expresses the degree of belief about a certain parameter in the form of a prior probability distribution. The normal bell-shaped distribution is an example of a probability distribution. This prior probability distribution is then combined with its likelihood of occurrence, forming a posterior probability distribution (posterior probability = prior probability X likelihood).
The end result of Bayesian analysis is the formation of a posterior probability distribution (Figure 1). It represents a revised or updated belief after taking new data into account. If there is lack of existing knowledge on the subject of interest, the researcher can still use Bayesian techniques. Here, the researcher is encouraged to use vague or uninformed prior probabilities.
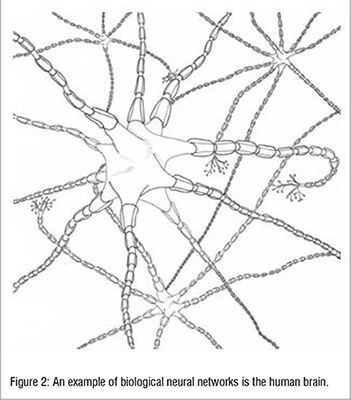
Artificial neural networks mimic biological neural systems. In biological systems, incoming dendrites collect signals which feed to the neuron (Figure 2). An electrical signal propagates along the axon with neurotransmitter discharge at the synapse.Examples of biologicalneural networks include the human brain and retina.
In artificial neural networks,input variablesconverge on a number of nodes. Nodes are grouped into layers. Layers are linked to each other via interconnection links. Between input and output layers, there can exist one or two hidden layers (Figure 3). Latent variables make up the hidden layer(s). In order to advance from one layer to the next, signals are processed via activation functions.
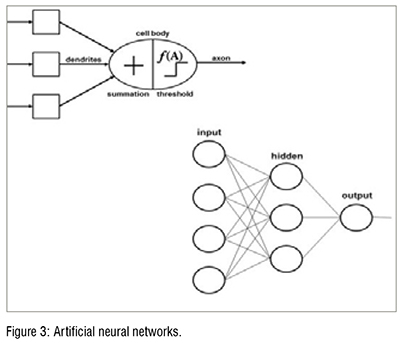
Artificial neural networks assume all or none logic. In the case of clinical outcome prediction, subjects are classified as having good or bad prognosis. Within each layer, nodes in the artificial neural network are connected with each other via connection links. Activation functions and associated weights are applied to these connection links.Artificial neural networks are intelligent systems that can learn and change behaviour by themselves as they gain experience. They also take into account latent variables or unobserved variables. These variables are not directly measured or accounted for during the design of the artificial neural network.
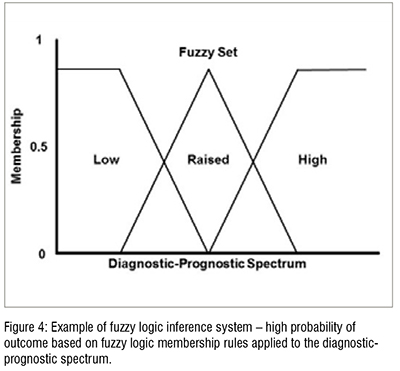
Fuzzy logic allows for uncertainty in disease diagnosis and prognosis. Fuzzy logic functions can carry any value from 0 to 1 (Figure 4). It, therefore, recognizes grey zones in diagnosis and prognosis, and registers diseases along a severity spectrum from mild to severe.One of the advantages of fuzzy logic is its explicit knowledge representation. The individual using fuzzy logic can:
1. specify inputs, control actions and outputs, and
2. clarify, or defuzzify, the entire process by adding crisp control actions, such as cutoff levels for diagnoses and prognoses, as well as trigger threshold levels for treatment.
By doing do, all actions in fuzzy logic can be accounted for (process of verification). Optimization is also achievable to create efficient fuzzy logic systems. Unlike artificial neural networks where learning is done by the networks themselves as they gain experience from datasets, fuzzy logic systems cannot train themselves. The designer derives all action commands manually in the form of “if-then” rules. The final fuzzy logic system can be represented in various ways, including equation or conceptual diagram formats.
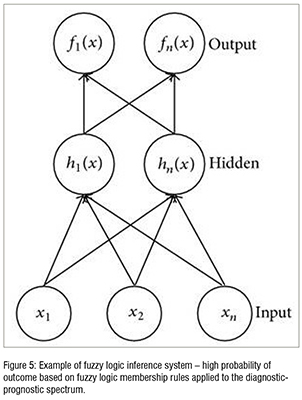
A multilayer perceptron artificial neural networks model is illustrated in Figure 5, where the output as follows:
Output = input to hidden layer + hidden layer to output layer
= activationfunction
*{sumof[(〖inputconnectionstohiddenlayer)〗_i )X〖weight〗_i ]+bias}
+{sumof[(〖hiddenlayerconnectiontooutputlayer)〗_j ) X〖weight〗_j ]
+biasterm}
If the activation function is the hyperbolic tangent function:
hidden unit j = hyperbolic tangent function × (bias term + sum of (weights from input unit i to hidden unit j × input unit i)), and
output = fn (x) = bias term + sum of (weights on connection from hidden unit j to output unit k ×hidden unit j).
In the Bayesian approach to artificial neural networks, the goal is to find the predictive distribution for target values in the new test case/model, given inputs for that case and inputs/targets in training cases. Here, the probability of data according to a particular model is an integral, representing the summation of all possible parameter values weighted by the strength of belief (as assigned by the researcher) in these parameter values. In a Bayesian neural network, the posterior probability density is proportional to the product of prior probability density and its associated likelihood, where the likelihood is the product of probabilities of data given parameters (weights and biases).
Principles of fuzzy logic, as discussed above, can then be applied to Bayesian neural networks. Here, all actions (verification) in fuzzy logic are accounted for, and optimization is achievable. Bayesian neural networks with fuzzy logic inferences can be represented as follows:
Expected outcome of function (fuzzy-Bayesian neural network)
= defuzzification technique applied to a Bayesian neural network
E(f)=defuzz [p(y_(n+1) |x_(n+1),(x_1,y_1 ),…,(x_n,y_n ))]
= defuzz [∫▒d θp(y_(n+1)│x_(n+1),θ)p(θ|(x_1,y_1 ),…,(x_n,y_n ))],
where defuzz can be max-min, centroid, left of mean, right of mean, or another defuzzification crisp control action rule.
Bayesian neural networks with fuzzy logic inferences can be applied to both clinical and non-clinical systems. In clinical outcome prediction using high dimensional data, Bayesian neural networks can be conceptually summarized as follows: Based on one’s own experience, one can specify (fuzzy logic) where along a spectrum of probabilities (provided by the Bayesian neural networks) the outcome lies. If the outcome falls outside the spectrum in real case scenario, the researcher is then encouraged to investigate unknown elements (latent variables) influencing the outcome variable in question.
Bayesian neural networks with fuzzy logic can be applied to both clinical and non-clinical settings. In clinical outcome prediction, it makes use of existing knowledge, recognizes unknown areas, incorporates one’s clinical reasoning and experience, as well as compensates for uncertainty in prognostication.
Illustrations are provided by medical illustrator, Aurora W.M. Lo, B.Com (Toronto) CPA (Illinois).
Benjamin W Y Lo is a Neurosurgeon and Neuro-ICU specialist. His clinical focus is cerebrovascular disorders. His research focus characterizes brain-body interactions in Neurocritical care patients with cerebrovascular disorders. Dr. Lo’s qualifications include FRCSC certification in Neurosurgery (2009), FRCSC certification in critical care medicine (2011), and MSc and PhD degrees in clinical epidemiology and biostatistics from McMaster University, Canada. His clinical experience includes working as a neurosurgeon and neuro- ICU specialist at St. Michael’s Hospital, University of Toronto; Montreal Neurological Institute & Hospital, McGill University; and Northwell Health Lenox Hill Hospital, Manhattan, New York.
